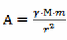ФИЗИКО -ТЕХНИЧЕСКАЯ ЛОБОРАТОРИЯ ГЛУШКО

PHYSICAL - TECHNICAL LABORATORY GLUSHKO

WE CHANGE THE FUTURE 
^{МЫ МЕНЯЕМ БУДУЩЕЕ}

ПРИНЦИП ЭКВИВАЛЕНТНОСТИ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ И СИЛЫ ИНЕРЦИИ.

Экскурс в историю.

По публикациям работ великого физика можно проследить все этапы становления общей теории относительности Эйнштейна. В 1911г. им впервые была высказана “гипотеза о физической природе гравитационного поля”, в которой универсальность гравитационной постоянной ещё только предполагалось каким-то образом использовать при создании новой теории тяготения. Он пишет, что ещё со времён Галилея универсальность этой постоянной “…следует из того опытного факта, что все тела в таком поле ускоряются равномерно и одинаково сильно. Этот опытный факт об одинаковом ускорении падения всех падающих в гравитационном поле тел является одним из наиболее общих фактов, установленных нами из наблюдений; несмотря на это, закон этот не нашёл ещё отражения в основах нашей физической картины мира” [1].

________________________________________________________________

Далее Эйнштейна заключает, что с его точки зрения универсальность постоянной тяготения позволяет заменить поле сил гравитационного притяжения тел на поле сил инерции. Действительно, силы инерции зависят только от величины ускорения тел и их массы. На них не влияет ни форма тела, ни температуры, ни то, из какого вещества состоят тела. Иными словами, на любые объекты, помещённые в систему отсчёта, движущуюся с ускорением, будут действовать силы инерции, пропорциональные только их массам, то есть точно так, как если бы эти тела были бы помещены в однородное поле тяготения. И далее он заключает: “Приняв это, мы получаем принцип, имеющий большое эвристическое значение, если он действительно справедлив. В самом деле, с помощью теоретического изучения явлений, протекающих относительно ускоренной координатной системы, мы получаем представление о ходе явлений в однородном гравитационном поле” [1].

Действительно, на этом основании законы движения тел в полях тяготения непосредственно сводятся к законам движения тел в неинерционных системах отсчёта. А поскольку кинематика и динамика ускоренного движения тел достаточно хорошо изучены в классической механике, то это обстоятельство позволяет без каких-либо особых проблем, с помощью только одного математического формализма, выявить дополнительные особенности к известным закономерностям движения тел в полях тяготения. Иными словам, к тем законам гравитации, которые были установлены ещё Ньютоном, как результат обобщения огромного экспериментального материала наблюдений за движением планет, можно будет добавить нечто новое о тяготении, полученное в ходе математических операций над функциональными зависимостями движения тел. То есть, как говаривал великий механик, “не измышляя никаких гипотез” о внутренних причинах гравитации, а надеясь только на математику, которая будто бы сама по себе “знает” всё о природе в целом, открыть с её помощью не только новые явления, свойства и закономерности могучей силы, управляющей движением звёзд и галактик, но и проникнуть в тайну её физической сущности.

В 1912г Эйнштейн укрепляется в своём мнении, что выбранный им путь решения проблемы тяготения, правильный. Он пишет: “По моему мнению, гипотеза о том, что “поле ускорения” является частным случаем гравитационного поля, по крайней мере настолько правдоподобна, особенно при учёте уже полученных в первой работе результатов относительно гравитационной массы энергии, что следует предпринять детальное исследование тех следствий, к которым приводит этот принцип эквивалентности” [2].

В 1913г Эйнштейн окончательно формулирует основные принципы, на которых должна строится его теория тяготения. К ним он относит:

“….1. Выполнение законов сохранения импульса и энергии.

2. Равенство инертной и тяжёлой масс замкнутых систем.

3. Справедливость теории относительности (в более узком смысле), т.е. системы уравнений должны быть ковариантны относительно линейных ортогональных подстановок (обобщённые преобразования Лоренца).

4. Наблюдаемые законы природы не должны зависеть от абсолютных значений гравитационного потенциала (или гравитационных потенциалов)….”[3].

Всё казалось “безоблачным на небе” новой гипотезы, но многие исследователи стали указывать на то, что силы инерции непосредственно связаны с понятием абсолютного пространства Ньютона, которое он ввел, прежде всего, для объяснения ускорений. Равномерное прямолинейное движение, согласно ньютоновской механике, относительно. Движение инерциальных систем происходит только относительно друг друга. Ускорение же абсолютно. Неинерциальные системы, по Ньютону, движутся ускоренно относительно некоторой привилегированной системы отсчета – абсолютного пространства. Возникла ситуация состоящая в том, что привлекая принцип эквивалентности масс к созданию новой теории гравитации Эйнштейн, тем самым, вступал в конфликт с созданной им специальной теорией относительности. Действительно, эта теория принципиально отвергала идею существования выделенной системы отсчёта – абсолютное пространство. Законы движения тел в инерциальных системах отсчёта, в согласии с ней, одни и те же и описываются одними и теми же уравнениями, т.е. должны быть ковариантными. Тогда как принцип эквивалентности масс основывался именно на существовании абсолютного пространства, поскольку ускорения абсолютны.

Возникла дилемма, выход из которой уже был подсказан Эрнстом Махом, австрийским физиком и философом. В своей “Механике”, (1883) отказавшись о ньютоновских абсолютных пространства, времени и движения, он впервые предпринял попытку построить механику, исходя только из того, что движения тел могут быть определены лишь по отношению к другим телам (тем самым сохранялся принцип относительности). Иными словами в пространстве, где нет никаких других тел, кроме пробного, последнее лишено сил инерции, то есть оно неспособно сопротивляться изменению своего состояния движения под действием сторонней силы. По идее Маха только массы всех тел вселенной создают силы инерции и, как принято сейчас говорить, эти массы инициируют не что иное, как реакцию “горизонта далёких звезд” на стороннюю силу, действующую на тело.

В своей работе 1914г “Формальные основы общей теории относительности” Эйнштейн апеллирует именно к Маху, утверждая, что “Если ньютоновские законы механики и гравитации не допускают такой интерпретации, то это можно считать скорее недостатками этих теорий” [4]. Таким образом была как бы спасена не столько специальная теория относительности, а сколько сама идея принципа относительности, являвшаяся путеводной звездой на протяжении всей научной жизни великого релятивиста.

В последующие годы, вплоть до 1916г, года окончательной редакции общей теории относительности, Эйнштейн в своих статьях расширяет, обосновывает и защищает от нападок 4 приведённых выше принципа её построения. На первое место, или точнее, основным из них становится принцип относительности. “Законы физики должны быть составлены так, чтобы они были справедливы для произвольно движущихся координатных систем. Таким образом мы приходим к расширению постулата относительности”. И далее он заключает: “Из этих соображений видно, что построение общей теории относительности должно одновременно привести и к теории тяготения, ибо гравитационное поле можно “создать” простым изменением координатной системы” [5].

Если вдуматься в смысл слов, цитируемых выше положений, то начало первой цитаты о том, что “Законы физики должны быть составлены так…” вызывает невольное ощущение навязывания физических законов самой природе. Не выявление законов, как последовательного результата исследований свойств природы, а именно диктовка законов ей, поскольку законы должны быть именно такими, какими их вывел математик.

Превалирование в физике метода математического феноменализма в поиске нового знания, над методом аналогий, с его непременным атрибутом – гипотезой, есть проблема науки и сегодняшних дней. И Эйнштейн, как физик-теоретик не мог не сталкиваться с ней, но именно как физик-теоретик он считал, что если исходные положения теории верны, то математика не ошибается, выводя новые соотношения между физическими величинами с помощью своего формализма. Отстаивая свою позицию он писал: “Из сказанного ясно, что теория относительности вовсе не является средством для вывода ещё неизвестных законов природы из ничего. Она даёт лишь универсально применимый критерий, ограничивающий число возможностей; в этом отношении её можно сравнить с законом сохранения энергии или со вторым началом термодинамики” [6]. Но согласитесь, что контекст этой цитаты точно такой же, как и приведённых выше, поскольку именно математик и никто иной на основе своих принципов и постулатов, с помощью математического аппарата выводит правильный закон и без сомнений приписывает его существование самой природе.

Как резюме экскурсу в историю создания общей теории относительности (ОТО) сделаем несколько замечаний по нему в целом, как говорится, с высоты знаний, накопленных физикой наших дней. Из тех 4 положений, которые хотел реализовать Эйнштейн в своей теории тяготения, осталось только два. Первым рухнул, как ни странно, первый принцип, а именно: “ Выполнение законов сохранения импульса и энергии”. Не сохраняются эти величины в теории тяготения. Здесь нам уместно сослаться на работу Гильберта, который, как и Э.Шредингер (современники Эйнштейна), впервые обнаружил указанные общефизические противоречия в теории гравитации Эйнштейна. Он писал: “… я утверждаю…, что для общей теории относительности, т.е. в случае общей инвариантности гамильтоновой функции, уравнений энергии, которые … соответствуют уравнениям энергии в ортогонально-инвариантных теориях, вообще не существует…” (цит. по книге: Визгин В.П. Развитие взаимосвязи принципов инвариантности с законами сохранения в классической физике. М., Наука, 1972, с.158). ). А вот другой пример. Академик А.А. Логунов, спасая закон сохранения энергии в теории гравитации Эйнштейна, разработал свою, как он утверждает, физическую теорию гравитационного поля. В широко известной монографии, “Релятивистская теория гравитации”, М., Наука, 1989, полностью посвященной именно этой проблеме, он пишет: “.., что в ОТО в принципе невозможны законы сохранения энергии-импульса и момента количества движения вещества и гравитационного поля, вместе взятые”. А поскольку закон сохранения энергии и импульса напрямую связаны с системой решения общековариантных уравнений гравитации, то вопрос о справедливости принципа относительности, т.е. когда системы уравнений должны быть ковариантны относительно линейных ортогональных подстановок, так и остаётся открытым. А это именно тот третий постулат, который был положенный в основание ОТО.

Принцип эквивалентности как таковой.

Далее, в этой статье, мы поведём разговор о втором постулате ОТО, с которого и началось само рождение теории тяготения Эйнштейна, то есть с “Равенства инертной и тяжёлой масс замкнутых систем”. Здесь существует несколько проблем, которые достаточно сильно переплетены между собой, входя в понятие принципа эквивалентности, и которые до настоящего момента времени так ещё и не решены. Первая из них, это вопрос о независимости массы тела от величины напряженности гравитационного поля (или потенциала), в котором она расположена. Действительно, никто теоретически не обосновывал, а тем более экспериментально не проверял, что при изменении напряженности поля тяготения величина массы не меняется. Например, если напряженность поля тяготения, в котором расположено тело, увеличится в два раза, то возрастет ли точно в два раза сила гравитации, действующая на его массу. А что, если это обстоит совершенно другим образом и здесь есть какая-то функциональная зависимость? С другой стороны не решена проблема независимости массы от величины ускорения. Здесь та же ситуация, аналогичная первой проблеме. Например, при увеличении силы в несколько раз, которая действует на то же самое тело, возрастет ли во столько же раз величина его ускорения? Сохраняет ли масса в этом случае свой статус коэффициента пропорциональности во втором законе Ньютона? Или она всё же зависит от величины ускорения, как она зависит от величины скорости? И есть ли здесь аналогичный предел величины ускорения, когда эта зависимость становится заметной, как это обнаружено для скорости? Это положение так же остаётся без обоснования и опытной проверки. И только после получения ответов на эти вопросы можно, в какой-то степени обосновано, подойти к решению проблемы истинности принципа эквивалентности масс.

И так перед нами принцип эквивалентности, как он понимается в современной физике, то есть гипотеза о том, что поле сил гравитационного притяжения тел можно заменить на поле сил инерции, возникающих в неинерциальной системе отсчёта.

В общей теории относительности, приведённая выше идея получила название “слабого” принципа эквивалентности инерционной и гравитационной масс. Напомним, что в парадигме современной физики она базируются на утверждении об универсальности гравитационной постоянной. То есть на положении, подтверждённом рядом специальных экспериментов, что поле тяготения совершенно одинаково действует на разные тела, сообщая им одинаковые ускорения, независимо от их массы, химического состава и других свойств. Это с одной стороны, а с другой стоит утверждение (которое, как не странно, берётся априори), что одинаковые массы разных тел под действием одной и той же силы приобретают одинаковые ускорения. Это, видимо, происходит только потому, что во втором законе Ньютона никто не сомневался и не сомневается. Если великий механик записал, что масса есть ничто иное как постоянный коэффициент пропорциональности между силой и ускорением во всём возможном диапазоне сил, то никто не решался и решится высказать свои сомнения по этому поводу. Но с того момента времени, когда был открыт второй закон механики, “много воды утекло” и величины сил, с которыми теперь работают физики, возросли на десятки порядков, так что, видимо, уже настало время поднять этот вопрос.

Точная формулировка “слабого” принципа эквивалентности, гласит, что движение тел в поле тяготения и движение тел в отсутствии тяготения, но относительно ускоренной системы отсчёта, аналогичны. В рамках общей теории относительности указанная аналогия перерастает из положения об эквивалентности действия полей сил инерции и гравитации (в мысленных экспериментах с телом, которое помещено внутри ракеты), в утверждение об их прямой физической тождественности. Результатом развития идеи тождественности полей становится утверждение, что не только механическое движение, но и вообще все физические процессы в истинном поле тяготения, с одной стороны, и в ускоренной системе, в отсутствие поля тяготения, с другой, протекают по одинаковым законам. Это есть так называемый “сильный” принцип эквивалентности общей теории относительности. Иными словами данное утверждение означает, что в принципе нет никакой возможности каким-либо образом различать между собой эти два силовых поля.

Экспериментальная основа принципа эквивалентности.

В настоящее время критерием оценки истинности принципа эквивалентности является эксперимент по определению отношения величин ускорения свободного падения двух разных масс, измеренных в поле тяжести Земли или Солнца (7, 8). То есть не экспериментальная проверка утверждения о физической тождественности полей инерции и гравитации (гипотеза Эйнштейна), а опытная проверка универсальности гравитационной постоянной. Известны программы с другими критериями оценки адекватности принципа эквивалентности реальным физическим свойствам природы, например: по измерению прецессии релятивистского гироскопа, которые, к сожалению, до настоящего момента времени так и не были реализованы (9). Но и здесь вопрос не выходил за рамки универсальности гравитационной постоянной. Повторимся: надо чётко осознавать то, что вопрос об одинаковости ускорения падения тел в одном и том же поле тяготения и вопрос о физической тождественности поля сил инерции полю гравитации это две принципиально разные проблемы. Положительное решение первого вопроса позволяет утверждать только то, что гравитационная постоянная универсальна для всех тел. И не больше этого. Тогда как ответ на второй вопрос переводит свойство похожести движения тел в рассматриваемых полях в эквивалентность полей по всем их свойствам, в соответствии с их физической сущностью. Именно в прямом смысле понятия “эквивалентность” и следует понимать этот принцип, то есть когда силы инерции полностью приравнивают силам гравитации, полагают их равнозначными друг другу и полностью заменяющими друг друга во всех физических процессах.

Заметим, что сами экспериментаторы, фактически уточняя универсальность гравитационной постоянной, тем не менее, твердо заявляли о проверке якобы принципа эквивалентности, тем самым, как бы незаметно для себя и других, подменяя одно положение другим. В опытах, поставленных Бесселем, Этвешем, Зееманом, Саузером (современников Эйнштейна), проверялась именно универсальность гравитационной постоянной, как и во всех последующих экспериментах, вплоть до наших дней. Однако, в последних опытах, выполненных в точности по аналогичной схеме предшествующих экспериментов, уже заявляется проверка принципа эквивалентности, что, видимо, считается вполне естественным после опубликования гипотезы Эйнштейна. Встречаем мы это, например, в обосновании и методике опытов 1959 – 1963гг, выполненных Дике с сотрудниками, или в экспериментах 1971г. осуществлённых группой Брагинского, в которых фактически проверялась универсальность гравитационной постоянной для выбранной группы, состоящей из двух веществ. Да и сам автор общей теории относительности не делал здесь различий, поскольку обсуждая результаты опыта Этвеша и ссылаясь в основном именно на него, отмечал, что, по его мнению, дальнейшее экспериментальное уточнение “слабого” принципа эквивалентности более важно, нежели новые проверки совпадения с расчётами наблюдаемых вековых смещений перигелия Меркурия и отклонение лучей света в поле тяжести Солнца (10).

Принципиальная схема таких экспериментов (для конкретности рассмотрим два последних) состояла в следующем. На Земле был установлен очень чувствительный крутильный маятник, на концах коромысла которого укреплены две массы, изготовленные из различных веществ. Выбор веществ, из которых были изготовлены массы, в самых первых экспериментах, определялся максимальной разностью в величине плотности тел. Тогда как в двух последних экспериментах были взяты вещества из разных концов таблицы Менделеева. Обоснование такого выбора заключалось в том, что у таких веществ сильно различается число протонов и нейтронов в ядре и, как следствие, у них различный дефект масс. К тому же у них различные скорости движения электронов на близких к ядру орбитах, и, следовательно, различные релятивистские поправки к массе. А поскольку физики уже знали, что все вещества состоят из разного количества одних и тех же элементарных частиц, то плотность вещества здесь была уже ни причём, так как в свойстве аддитивности масс, начиная с Галилея, никто не сомневался. Таким образом, в этих опытах проверке подвергалось релятивистское соотношение между массой и энергией. В опытах Дике были выбраны алюминий и золото, а у Брагинского – алюминий и платина.

Экспериментаторы утверждали, что, если ускорения падения на Солнце у этих двух масс разные, то крутильный маятник немного развернётся. Из-за вращения Земли вокруг своей оси, через 12 часов, когда массы поменяются местами, предполагаемая разница в ускорениях развернёт маятник в противоположную сторону на ту же самую величину. Период вращательных колебаний маятника должен составлять 24 часа, а максимальные отклонения наблюдаться в полдень и в полночь. Эксперименты показали, что колебаний не было, результат был нулевой. Из этого факта делалось заключение, что ни только сравниваемые вещества, но и все без исключения тела, падают на солнце с одним и тем же ускорением. Причём точность сделанного вывода равнялась чувствительности экспериментальной установки. В опытах Брагинского относительная разница отношения ускорений для платины и алюминия была не больше 1·10-12. Это фантастическая по точности цифра.

Следует отметить, что даже в такой, казалось бы, простой методике и принципиальной схеме эксперимента, где всё прозрачно и обоснованно до мелочей, но при их анализе всё же возникает множество вопросов, которые сами экспериментаторы в своих методиках, отчётах и трактовках обошли вниманием. Вопросы не возникали бы, если б в опытах нить подвеса маятника располагалась бы перпендикулярно к направлению на Солнце. А фактически она находилась под углом к нему, поскольку у установок нить была строго перпендикулярна поверхности Земли, ось вращения которой наклонена к плоскости эклиптики, а сами установки были расположены на определённой широте земного шара. Как такое взаимное расположение объектов опыта могло влиять на экспериментальное устройство и его чувствительность авторы эксперимента не поясняют. К тому же этот угол постоянно изменялся в течение суток. А именно это обстоятельство, в теоретическом плане анализа методики опыта, должно было бы приводить к разложению предполагаемого момента сил на составляющие, одна из которых, лежащая в плоскости нити, должна была изгибать её. Анализа этого фактора в отчётах нет.

Но здесь важнее да же ни это, а другое обстоятельство. Так, даже если бы указанная перпендикулярность строго соблюдалась, то крутильный маятник все равно бы не вращался, поскольку момент сил, который должен был бы разворачивать маятник, экспериментаторами был уже уравновешен (скомпенсирован) в процессе изготовления и ввода устройства в работу. Действительно, в самом начале эксперимента (по данным отчётов) нить маятника не была закручена, то есть маятник не находилась под действием какого-либо внешнего момента сил, и он мог совершать свободные колебания в ту и другую сторону относительно своего “нулевого” положения. О периоде свободных колебаний маятника и о точном его значении, подтверждённом ходом специальных проверок, для всех перечисленных выше установок говорят сами экспериментаторы. А это означает, что, если в самый начальный момент опыта нить маятника была свободна, то есть она не была закручена предполагаемым моментом сил, то это положение будет сохраняться всегда, в течении всего 24 часового вращения планеты вокруг своей оси, поскольку момент сил уже был уравновешен в конструкции прибора. Иными словами, даже если бы сравниваемые массы падали на солнце с разными ускорениями (то есть предположить, что гравитационная постоянная не обладает свойством универсальности), то специальный разворот такого устройства в целом вокруг нити маятника или перенесение его в гравитационное поле другой напряженности не привели бы к возникновению ещё одного дополнительного нескомпенсированного момента сил, к тому моменту сил, который был уже уравновешен экспериментаторами.

Эту тонкость обстоятельств эксперимента постановщики опытов по проверке принципа “эквивалентности” просто не заметили. А она свела на нет все их старания и сделала такие опыты бессмысленными. Следовательно, реального экспериментального подтверждения гипотезы Эйнштейна просто нет.

Заметим, что с учётом сделанного нами замечания, постановка подобного рода опытов сопряжена с громадными методическими трудностями. Действительно, для получения положительного результата компенсировать момент нельзя. Но компенсировать надо, поскольку неизвестно его происхождение (любая незамеченная ошибка в изготовлении устройства может привести к закручиванию нити). А если скомпенсируешь, то тогда точно ничего не измеришь, поскольку всегда будет нулевой результат. Вот такая дилемма.

Остаётся одна лишь надежда, или на градиент сил, который возникает на длине плеча маятника, или какой-либо иной эффект, приводящий к асимметрии маятника при его вращении в гравитационном поле Солнца. Только при личной необходимости решения подобных экспериментальных задач становится осязаемой гениальность экспериментального творчества авторов безупречно выполненных опытов.

Новый критерий оценки истинности принципа эквивалентности.

Нами же предлагается новый критерий оценки истинности принципа эквивалентности, с помощью которого, как нам кажется, все же можно будет расставить все точки над “и” не только в вопросе о тождественности сравниваемых полей, он и в проблеме универсальности гравитационной постоянной. Суть критерия состоит в сравнении максимальной удельной энергетической мощности полей сил инерции и сил гравитации. Действительно, рассматриваемые поля являются силовыми, а поэтому могут совершать работу, изменяя состояние движения тел. Под удельной мощностью понимается работа, совершаемая полями в единицу времени, по изменению скоростей движения тел единичной массы. Поскольку понятие тождественности означает полное совпадение всех характеристик сравниваемых полей, то, следовательно, должно наблюдаться равенство и их удельных мощностей. В принципе, в соответствии с сутью нового критерия, должны сравниваться максимальные значения указанной характеристики силового поля, поскольку в наблюдаемых физических процессах зачастую рассматриваемые поля работают не на пределе своих возможностей.

В качестве примера можно рассчитать удельную мощность поля сил инерции, которая реализуется в процессе столкновения протонов встречных пучков Большого адронного коллайдера. При этом очевидно, что эта мощность не является максимальной, поскольку в природе есть аналогичные явления, протекающие с большей интенсивностью преобразования кинетической энергии при работе сил инерции. Например, такой случай может реализоваться при столкновении протонов космических лучей с атомами земной атмосферы. Действительно, кинетическая энергия протонов коллайдера ограничена величиной в 450 Гэв, тогда как в энергетическом спектре космических лучей присутствуют протоны с кинетической энергией в 1020 эв. Однако величину времени взаимодействия сталкивающихся протонов и полную энергию акта столкновения проще всего вычислить для коллайдера, поскольку при этом меньше всего делается допущений, требующих своего обоснования. Действительно, в первом приближении процесс столкновения протонов в коллайдере можно представить как неупругий лобовой удар двух шаров, летящих в нём навстречу друг к другу со скоростью близкой к скорости света. Такое допущение вполне возможно, поскольку из ядерной физики хорошо известен факт, что  работа электрических сил отталкивания одноимённых зарядов (протонов) по перемещению из бесконечности в точку пространства, где силы электрического отталкивания уступают ядерным силам притяжения, равна примерно 0,1 Мэв. На фоне кинетической энергии протонов коллайдера в 450 Гэв потеря ими энергии в 0,1 Мэв, связанная с преодолением электрического поля, не может существенно повлиять на результаты вычислений.
В этом случае вся кинетическая энергия двух шаров будет потрачена на их “деформацию”, конечным “продуктом” которой будет энергия образования и движения разлетающихся “осколков”. Очевидно, что время действия сил инерции определится как частное от деления диаметра шара на его скорость.

t = d/v (1)

Если за диаметр шара d принять среднеквадратичный диаметр протона (который в ядерной физике принят равным 1,6 Ферми, или 1,6·10^-15 м), а за скорость v шара взять скорость движения протона в Большим адронным коллайдером, которая близка к скорости света (для упрощения расчётов мы берём её равной скорости света, т.е. v = 3·10⁸ м/с, что незначительно может отразиться на результате вычислений), то время действия сил инерции в процессе столкновения будет равно

t = d/v = 1,6·10^-15 / 3·10⁸ = 0,53·10^-23 с. (2)

Не сложный расчёт показывает, что при энергии каждого протона, равной A=450 Гэв или 7,2·10-8 дж при столкновении силы инерции разовью мощность в

Wi = 2А/t =2 · 7,2·10^-8 /0,53·10^-23 = 2,7·10¹⁶ вт. (3)

При расчёте удельной мощности гравитационного поля, ускоряющего, как и в первом случае, протоны (для большей наглядности и облегчения процесса сравнения, условия вычисления мощности сил гравитационного поля должны быть сопоставимы с условиями вычисления мощности сил инерции), можно рассмотреть поле тяготения такого экзотического объекта вселенной, каким является “Черная дыра”. Вблизи своего гравитационного радиуса она обладает самым сильным полем тяготения из всех известных космических претендентов на этот титул. Именно в этом месте гравитационного поля “Чёрной дыры” работа сил тяготения по перемещению тел, отнесённая к единице длины  пути их движения, превосходит аналогичную работу этих же самых сил, выполненную ими в любом другом месте поля.

А поэтому, видимо, именно здесь имеет место случай с максимальным значением удельной мощности этого поля. К тому же данный астрономический объект более всего подходит для сравнения мощностей рассматриваемых полей, поскольку именно здесь протоны движутся так же со скоростями, близкими к скорости света. А поэтому мы вправе время ускорения протонов в поле тяготения черной дыры (в области её гравитационного радиуса) взять равным времени действия сил инерции, возникающих при столкновении протонов в Большом адроном коллайдере. Иными словами, работу сил гравитационного поля можно будет вычислить по разности потенциалов поля, между точками, лежащими на его радиус-векторе, находящимися на расстоянии, равном диаметру протона, по формуле:

                           ·d = 8,86·10^-30 дж, (4)

где: гравитационная постоянная γ = 6·10^-11 м3/кг·с2,

масса Солнца М = 19,89·10²⁹ кг,

гравитационный радиус Солнца r = 6·10³ м,

масса протона m = 1,67·10^-27 кг,

диаметр протона d = 1,6·10^-15 м.

Таким образом, для черной дыры с массой Солнца мощность гравитационного поля в районе её гравитационного радиуса, то есть отношение работы поля, связанной с ускорением протона, ко времени действия ускорения равного 0,53·10^-23 с (напомним, что это время равно времени действия сил инерции в Большом адроном коллайдере), будет равна

Wg = 2А/t =2 · 8,86·10^-30 / 0,53·10^-23 = 1, 67·10^-6 вт. (5)

Таким образом, отношение удельной мощности поля сил инерции к удельной мощности сил гравитационного поля будет равно

Wi / Wg = 2,7·10¹⁶ /1, 67·10^-6 ≈ 1,6·10²². (6)

Полученная огромная величина отношения мощностей указывает на то, что ни о какой тождественности этих полей не может быть и речи. Даже если мы ошиблись в допущениях при вычислении мощности сравниваемых полей на прядки (что тут мелочится), то цифра с двадцатью двумя нулями говорит сама за себя. То есть силы инерции и силы гравитации по своей физической сути разнятся не только по тем явлениям, в которых они участвуют в роли главных атрибутов физического процесса (гравитация и динамика движения тел в пространстве), но и по их энергетике. Причём, максимальная энергетическая мощность гравитационных полей лежит в самом начале диапазона возможных мощностей сил инерции. А поскольку диапазоны мощностей сил не совпадают, следовательно, утверждение об их эквивалентности лишено всякого смысла. Иными словами, если (на основании предположения истинности “слабого” принципа эквивалентности) попытаться представить астрономический объект с напряженностью поля тяготения, которое было бы эквивалентно полю сил инерции не инерциальной системы отсчета, движущейся с величиной ускорения сталкивающихся протонов Большого адронного коллайдера, то его не сможет вообразить даже самый ярый сторонник общей теории относительности, обладающий самым незаурядным раскрепощённым воображением.

Наша гипотеза.

Огромная величина отношения мощностей, и как следствие её логического развития, приводит к гипотезе, позволяющей указать пути подхода к решению важнейших проблем физики, связанных с понятиями массы тела и субстанциональностью пространства.

Напомним, что общепринято было полагать, что: поскольку тело и его масса могут инициировать, как силы инерции, так и тяготения, в которых сама масса является главной характеристикой этих, существенно разных, физических процессов, то между величинами сил должна соблюдаться определённая пропорциональность. Такое утверждение соответствует физической логике. Причём, пропорциональность должна наблюдаться именно в случае, когда тело одновременно участвует в обоих процессах, то есть находиться под одновременным действием этих сил. Это особый и очень частный случай, поскольку до настоящего момента времени полагалось, что диапазоны возможных значений сил инерции и тяготения пропорциональны друг другу.

Однако, огромная величина отношения мощностей указывает на то, что инерционная характеристика массы тела является определяющей, в сравнении с гравитационной, то есть именно инерционная масса содержит в себе все свойства и особенности физического понятия “массы” тела. Иными словами, тот же самый внутренний механизм понятия “масса тела”, который обеспечивает образование сил инерции и он же самый, без каких-либо изменений, обеспечивает и образование сил тяготения, поскольку диапазоны возможных значений сил инерции и тяготения не пропорциональны друг другу. Причём диапазон возможных значений сил тяготения занимает незначительное место в самом начале диапазона сил инерции.

Это же обстоятельство следует и из другого факта. Силы инерции возникают, как в пространстве, в котором нет никаких других силовых полей (гравитационных, электрических, магнитных и т.д.), так и работают в нём совместно с другими силовыми полями. Тогда как силы тяготения действуют на массу тела только при наличии гравитационного поля. К тому же следует учесть, что силы инерции обеспечиваются кинетической энергией тела, которая сосредоточена в самом теле, и именно в объеме пространства, занимаемом его массой. Образно говоря – без энергии нет силы. В пространстве, окружающем движущееся тело, этой энергии нет. Только поэтому ещё со времён Ньютона полагали, что “механизм” образования сил инерции – это масса тела, который проявляет себя во взаимодействии тела с субстанциональным пространством, поскольку ускорения абсолютны. Второй закон Ньютона – это закон взаимодействия тела именно с таким с пространством, где массе отведена роль константы взаимодействия с пространством. В абсолютно пустом пространстве, лишённом каких-либо физических свойств, нет оснований для возникновения сил инерции, то есть, не взаимодействуя ни с чем, тело не может “сопротивляться” действию сторонней силы, изменяющей его состояние движения.

Тогда как гравитационное поле распределено в пространстве, в котором расположено инициирующее его тело, и в этом смысле, само пространство обладает некоторым количеством энергии. И именно поэтому оно способно в тех местах, где находятся другие тела, образовывать силы тяготения. Без энергии нет силы. Огромная величина отношения удельных мощностей сравниваемых полей указывает на то, что гравитационные силы это не что иное, как процесс взаимодействия инерционной массы (в нашем случае просто массы) с пространством, которое несколько изменено гравитирующей массой, поскольку сам механизм взаимодействия инерционной массы с таким пространством остаётся прежним. Иными словами поле тяготения это не обособленный объект природы или особая субстанция, размещённая в пространстве, это одно из возможных состояний самого пространства (в этом положении усматривается прямая аналогия с общей теорией относительности).

Из сделанного предположения (гипотезы) вытекают следующие выводы. Поскольку взаимодействие тела с пространством обеспечивается только инерционной массой в не зависимости от того есть в нём гравитационное поле или нет, то ускорение свободного падения разных масс для разных тел в гравитационном поле другого тела будет одним и тем же (универсальность гравитационной постоянной). Более того, на том же самом основании, в полях тяготения разной напряженности одна и та же масса тела, находящаяся в одном и том же состоянии движения, под воздействием одной и той же сторонней силы всегда будет испытывать одно и то же ускорение. Тогда как обратное утверждение уже не столь очевидно, а именно: при разных величинах скоростей и ускорений, возникающих под действием сторонних сил (не гравитационных), одно и то же тело (масса), помещённая в поле тяготения одной и той же напряженности, уже не будет испытывать одну и ту же гравитационную силу. Здесь уместно вспомнить о забытых экспериментах Этвеша, который сделал свою установку подвижной. В этих опытах он показал, что тело, движущееся в направлении с запада на восток (скорость движения которого складывается со скоростью вращения Земли), весит немного меньше, чем тело, движущееся в противоположном направлении (эффект Этвеша) [11].

Это связано с тем, что отношение диапазонов мощностей сил гравитации и инерции (как и действующих величин самих сил), разнятся на десятки порядков, а поэтому это доминирование сил инерции должно накладывать свой отпечаток на действие сил гравитации, образуя функциональную зависимость сил тяготения от величины скорости и ускорения тела. Иными словами мы можем говорить о функциональной зависимости отношения гравитационного заряда тела к его массе от скорости и ускорения движения тела. Тогда как (повторимся) существующая парадигма принципа эквивалентности содержит в себе противоположное утверждение, что весь диапазон сил поля инерции, соответствует всему диапазону сил поля тяготения, и коэффициент пропорциональности между гравитационной и инерционной массами является константой (равен единице). То есть он не является функцией величины напряженности поля тяготения, а тем более поля сил инерции.

Сделанное предположение позволяет утверждать, что, например, вращение тел в поле тяготения будет приводить к эффекту “увеличения” их массы за счёт изменения величины коэффициента пропорциональности межу силами инерции и гравитации, одновременно действующими на одну и ту же массу (релятивистские гироскопы). Аналогичный эффект будет происходить и при поступательном движении одного и того же тела в поле тяготения, движущегося с разными скоростями или изменяющим свою скорость под действием сторонних сил.

Подобное утверждение можно сделать и относительно других силовых полей – электрического и магнитного. Действительно, силы инерции по своей интенсивности воздействия на материю и при тех же пространственно-временных масштабах (~ 10^-13см, ~ 10^-23с), с которыми обычно имеют дело в атомных ядрах, по величине сопоставимы с сильным взаимодействием ядерных сил и, вероятнее всего, значительно превосходят последние, а тем более силы, возникающие в электрических и магнитных полях (только поэтому был построен Большой адронный коллайдер). Следовательно, если предположить, что механизм их действия на заряженные тела аналогичен механизму образования сил тяготения, то в этих полях должны наблюдаться подобные эффекты. То есть с ростом величины скоростей и ускорений, которые действуют на заряженные частицы, движущиеся в этих полях, отношение заряда частицы к массе будет изменяться за счёт изменения коэффициента пропорциональности между силами инерции и электрическими и магнитными силами.

По сути, опыты по изучению движения однотипных заряженных частиц в магнитных и электрических полях показали увеличение их масс с ростом скорости их движения. Общепринятое объяснение данного явления связано с релятивистским эффектом специальной теории относительности. Однако следует обратить внимание на то, что в экспериментальных установках, с помощью которых был открыт этот эффект, движение частиц в них происходило в полях одной и той же напряжённости. Но если, при одной и той же скорости движения изменять напряженность силового поля, отклоняющего частицу, то это обстоятельство будет приводит к существенному изменению величины центробежных ускорений и времени их действия на частицу и, как следствие, приведёт к изменению величины коэффициента пропорциональности между зарядом и массой. Не вызывает сомнений, что будут разработаны методики постановки экспериментов, которые позволят сделать выбор между факторами, влияющими на степень отклонения частиц в силовых полях. То есть с целью получения четко доказательства того с чем конкретно это связано: или с релятивистским увеличением массы частицы, или с изменением величины коэффициента пропорциональности между зарядом и массой. Если факт изменения величины пропорциональности сил будет экспериментально подтверждён, то это обстоятельство будет неоспоримым доказательством реальности существования субстанционального пространства.

К сожалению, авторы не смогли найти литературных источников с результатами специальных исследований по этой проблеме. Публикуемые в печати работы о том, что вес гироскопа зависит о того, вращается он или неподвижен, хотя и прямо касается именно этой тематике, но, по мнению самих исполнителей экспериментов, решает совершенно иные физические проблемы, а поэтому поднятые нами вопросы в них не нашли никакого отражения.

Особо отметим тот факт, что возникновение сил инерции изначально объясняли результатом взаимодействия массы тела с абсолютным пространством (ускорения абсолютны). В современной физике, в связи с созданием специальной теории относительности, от идеи субстанционального пространства отказались. Однако уже известны несколько абсолютных систем отсчёта, реанимирующих эту старую идею, которые связывают с такими материальными телами вселенной, как, например, межгалактическое реликтовое излучение (так называемый новый электромагнитный эфир) или гравитационными полями звёзд, образующими метрику мирового пространства, каждой точке которой приписывается строго определенная физическая величина – кривизна пространства. И более того, всё тот же пресловутый “горизонт далеких звезд” Маха фактически выделяет в каждой точке пространства одну “покоящуюся” (в среднем относительно этой далекой материи) систему координат. Поэтому в рамках этой работы будет естественным высказать ещё одну новую идею, доказывающую субстанциональность пространства. Она основана на общих свойствах симметрии (по аналогии с классической термодинамикой), которая позволяет утверждать, что суммарный импульс движения всех материальных тел вселенной, в системе отсчёта абсолютного пространства, должен быть равен нулю. При этом суммарный импульс тех же самых объектов, подсчитанный в системе отсчёта, связанной с каким-то одним из этих тел, будет точно равен импульсу этого тела в системе абсолютного пространства. Иными словами, подсчитывая импульс достаточно большого количества космических объектов, наблюдаемых с поверхности нашей планеты, можно с точностью эксперимента вычислить абсолютную скорость её движения. В случае успеха при реализации этой идеи будет получено ещё одно доказательство реальности существования субстанционального пространства. Уверенность в истинности его существования значительно возрастает, если учитывать, что в классической механике закон сохранения импульса обычно выводится из законов механики Ньютона, как их следствие. При этом напомним, что сами законы Ньютона отражают собой механизм взаимодействия материальных тел с абсолютным пространством, что не противоречит их статусу законов движения тел в инерциальных замкнутых системах отсчёта.

Как резюме всему вышесказанному констатируем, что в представленной парадигме взглядов на проблему соотношения материальных тел с пространством, а так же массы тела и сил инерции, предложенный энергетический подход совершенно по иному расставляет акценты в ранге всех известных силовых взаимодействий и их значимости в описании физической картины мира. Силы инерции и обеспечивающая их масса тела выдвигаются на её передний план, где под массой тела подразумевается только её инертная характеристика. И, как следствие, реальность существования сил инерции требует наличия реальности субстанционального пространства, что сопряжено со всеми тяжёлыми последствиями для современной парадигмы физического знания, основанного на идеях релятивизма.

Литература:

А.Эйнштейн. Собрание научных трудов. М.1965. стр.166-167.
Эйнштейн. Собрание научных трудов. М.1965. стр.189.
Эйнштейн. Собрание научных трудов. М.1965. стр.275.
Эйнштейн. Собрание научных трудов. М.1965. стр.327.
А.Эйнштейн. Собрание научных трудов. М.1965. стр.456-457.
А.Эйнштейн. Собрание научных трудов. М.1965. стр.388.
F.Witteborn, W.Fairbank, Phys. Rev. Lett. 19,1049. 1967.
В.Б.Брагинский, А.Б.Манукин, Измерение малых сил в физических экспериментах. Изд. Наука, М. 1974
F. Everitt, W.Fairbank, Proc. of the Conference on Experimental Tests of Gravitational Theories, Caltech, 1971.
V.L.Ginzburg, Astronautica Acta 12, № 2, 136,1966.
R.H.Diecke, The Eotvos Experiment, Scientific American 205 (6), 84 (1961).

Дата публикации: 23 ноября 2009 

© 1993 - 2025 glushko.us